Example Tetrahedral Grid

This section defines structure types for describing the grid coordinates, element data, and flow solution data pertaining to a zone. Entities of each of the structure types defined in this section are contained in the Zone_t structure.
The physical coordinates of the grid vertices are described by the GridCoordinates_t structure. This structure contains a list for the data arrays of the individual components of the position vector. It also provides a mechanism for identifying rind-point data included within the position-vector arrays.
GridCoordinates_t< int IndexDimension, int VertexSize[IndexDimension], int PhysicalDimension> :=
{
DataArray_t<DataType,PhysicalDimension, 2> BoundingBox ; (o)
List( Descriptor_t Descriptor1 ... DescriptorN ) ; (o)
Rind_t<IndexDimension> Rind ; (o/d)
List( DataArray_t<DataType, IndexDimension, DataSize[]>
DataArray1 ... DataArrayN ) ; (o)
DataClass_t DataClass ; (o)
DimensionalUnits_t DimensionalUnits ; (o)
List( UserDefinedData_t UserDefinedData1 ... UserDefinedDataN ) ; (o)
} ;
Notes
GridCoordinates_t requires two structure parameters: IndexDimension identifies the dimensionality of the grid-size arrays, and VertexSize is the number of vertices in each index direction excluding rind points. For unstructured zones, IndexDimension is always 1 and VertexSize is the total number of vertices, excluding rind points.
The grid-coordinates data is stored in the list of DataArray_t entities; each DataArray_t structure entity may contain a single component of the position vector (e.g., three separate DataArray_t entities are used for x, y, and z).
Standardized data-name identifiers for the grid coordinates are described in Conventions for Data-Name Identifiers.
Rind is an optional field that indicates the number of rind planes (for structured grids) or rind points (for unstructured grids) included in the grid-coordinates data. If Rind is absent, then the DataArray_t structure entities contain only "core" vertices of a zone; core refers to all interior and bounding vertices of a zone - VertexSize is the number of core vertices. Core vertices in a zone begin at [1,1,1] (for a structured zone in 3-D) and end at VertexSize. If Rind is present, it will provide information on the number of "rind" points in addition to the core points that are contained in the DataArray_t structures. Indices in DataArray_t structures have the range [1 - a,1 - c,1 - e] to [II + b,JJ + d,KK + f] where VertexSize = [II,JJ,...] and RindPlanes = [a,b,...] (see the Rind_t structure for the definition of RindPlanes).
DataClass defines the default class for data contained in the DataArray_t entities. For dimensional grid coordinates, DimensionalUnits may be used to describe the system of units employed. If present, these two entities take precedence over the corresponding entities at higher levels of the CGNS hierarchy, following the standard precedence rules. An example that uses these grid-coordinate defaults is shown under Grid Coordinates Examples.
The UserDefinedData_t data structure allows arbitrary user-defined data to be stored in Descriptor_t and DataArray_t children without the restrictions or implicit meanings imposed on these node types at other node locations.
The BoundingBox array is optional and provides a measure within which all the grid points lie. It stores minima and maxima of Coordinates values sorted by alphabetical order for Cartesian and Cylindrical coordinate systems while Spherical and Auxiliary coordinate systems retain a specific order to be coherent with the existing SIDS notation:
| System | Bounding Box | |
|---|---|---|
| Cartesian 3-D |
[[Min(CoordinateX), Min(CoordinateY), Min(CoordinateZ)],
[Max(CoordinateX), Max(CoordinateY), Max(CoordinateZ)]]
|
|
| Cylindrical 3-D |
[[Min(CoordinateR), Inf(CoordinateTheta), Min(CoordinateX)],
[Max(CoordinateR), Sup(CoordinateTheta), Max(CoordinateX)]] or
[[Min(CoordinateR), Inf(CoordinateTheta), Min(CoordinateY)],
[Max(CoordinateR), Sup(CoordinateTheta), Max(CoordinateY)]] or
[[Min(CoordinateR), Inf(CoordinateTheta), Min(CoordinateZ)],
[Max(CoordinateR), Sup(CoordinateTheta), Max(CoordinateZ)]]
|
|
| Spherical |
[[Min(CoordinateR), Inf(CoordinateTheta), Inf(CoordinatePhi)],
[Max(CoordinateR), Sup(CoordinateTheta), Sup(CoordinatePhi)]]
|
|
| Auxiliary 3-D |
[[Min(CoordinateXi), Min(CoordinateEta), Min(CoordinateZeta)],
[Max(CoordinateXi), Max(CoordinateEta), Max(CoordinateZeta)]]
|
|
Thus, all coordinate systems are handled in a deterministic way. For 2-D coordinate system, the order is kept the same as for 3-D.
Angle coordinate part of a bounding box is defined by Inf(CoordinateTheta) and Sup(CoordinateTheta) (respectively Inf(CoordinatePhi) and Sup(CoordinatePhi) for spherical coordinate angle) where Inf and Sup operators ensure unicity of the angle interval. The constraints for valid angle bounding box limits are:
GridCoordinates_t requires a single structure function, named DataSize, to identify the array sizes of the grid-coordinates data. A function is required for the following reasons:
if (Rind is absent) then
{
DataSize[] = VertexSize[] ;
}
else if (Rind is present) then
{
DataSize[] = VertexSize[] + [a + b,...] ;
}
where RindPlanes = [a,b,...] (see the
Rind_t structure for the
definition of RindPlanes).
This section contains examples of grid coordinates. These examples show the storage of the grid-coordinate data arrays, as well as different mechanisms for describing the class of data and the system of units or normalization.
This example uses Cartesian coordinates for a 2-D grid of size 17 × 33; the data arrays include only core vertices, and the coordinates are in units of feet.
! IndexDimension = 2
! VertexSize = [17,33]
GridCoordinates_t<2, [17,33]> GridCoordinates =
{{
DataArray_t<real, 2, [17,33]> CoordinateX =
{{
Data(real, 2, [17,33]) = ((x(i,j), i=1,17), j=1,33) ;
DataClass_t DataClass = Dimensional ;
DimensionalUnits_t DimensionalUnits =
{{
MassUnits = MassUnitsNull ;
LengthUnits = Foot ;
TimeUnits = TimeUnitsNull ;
TemperatureUnits = TemperatureUnitsNull ;
AngleUnits = AngleUnitsNull ;
}} ;
}} ;
DataArray_t<real, 2, [17,33]> CoordinateY =
{{
Data(real, 2, [17,33]) = ((y(i,j), i=1,17), j=1,33) ;
DataClass_t DataClass = Dimensional ;
DimensionalUnits_t DimensionalUnits =
{{
MassUnits = MassUnitsNull ;
LengthUnits = Foot ;
TimeUnits = TimeUnitsNull ;
TemperatureUnits = TemperatureUnitsNull ;
AngleUnits = AngleUnitsNull ;
}} ;
}} ;
}} ;
From the Conventions for Data-Name Identifiers,
the identifiers
for x and y are CoordinateX and CoordinateY,
respectively, and both have a data type of real.
The value of DataClass
in CoordinateX and CoordinateY indicate the data is
dimensional, and
DimensionalUnits
specifies the appropriate units are feet.
The DimensionalExponents
entity is absent from both CoordinateX and CoordinateY;
the information that x and y are lengths can be inferred
from the data-name identifier
conventions for coordinate systems.
Note that FORTRAN multidimensional array indexing is used to store the data; this is reflected in the FORTRAN-like implied do-loops for x(i,j) and y(i,j).
Because the dimensional units for both x and y are the same, an alternate approach is to set the data class and system of units using DataClass and DimensionalUnits at the GridCoordinates_t level, and eliminate this information from each instance of DataArray_t.
GridCoordinates_t<2, [17,33]> GridCoordinates =
{{
DataClass_t DataClass = Dimensional ;
DimensionalUnits_t DimensionalUnits =
{{
MassUnits = MassUnitsNull ;
LengthUnits = Foot ;
TimeUnits = TimeUnitsNull ;
TemperatureUnits = TemperatureUnitsNull ;
AngleUnits = AngleUnitsNull ;
}} ;
DataArray_t<real, 2, [17,33]> CoordinateX =
{{
Data(real, 2, [17,33]) = ((x(i,j), i=1,17), j=1,33) ;
}} ;
DataArray_t<real, 2, [17,33]> CoordinateY =
{{
Data(real, 2, [17,33]) = ((y(i,j), i=1,17), j=1,33) ;
}} ;
}} ;
Since the DataClass and
DimensionalUnits
entities are not present in CoordinateX and CoordinateY,
the established rules for dimensional data
dictate that DataClass and DimensionalUnits specified
at the GridCoordinates_t
level be used to retrieve the information.
This example uses cylindrical coordinates for a 3-D grid whose core size is 17 × 33 × 9; the grid contains a single plane of rind on the minimum and maximum k faces. The coordinates are nondimensional.
! IndexDimension = 3
! VertexSize = [17,33,9]
GridCoordinates_t<3, [17,33,9]> GridCoordinates =
{{
Rind_t<3> Rind =
{{
int[6] RindPlanes = [0,0,0,0,1,1] ;
}} ;
! DataType = real
! IndexDimension = 3
! DataSize = VertexSize + [0,0,2] = [17,33,11]
DataArray_t<real, 3, [17,33,11]> CoordinateRadius =
{{
Data(real, 3, [17,33,11]) = (((r(i,j,k), i=1,17), j=1,33), k=0,10) ;
DataClass_t DataClass = NormalizedByUnknownDimensional ;
}} ;
DataArray_t<real, 3, [17,33,11]> CoordinateZ = {{ }} ;
DataArray_t<real, 3, [17,33,11]> CoordinateTheta = {{ }} ;
}} ;
The value of RindPlanes specifies two rind planes on the
minimum and maximum k faces.
These rind planes are reflected in the structure function
DataSize which is equal to the number
of core vertices plus two in the k dimension.
The value of DataSize is passed to the
DataArray_t entities.
The value of DataClass
indicates the data is nondimensional.
Note that if DataClass is set as
NormalizedByUnknownDimensional at a higher level
(CGNSBase_t or
Zone_t), then it is not
needed here.
Note that the entities CoordinateZ and CoordinateTheta are abbreviated.
This example uses Cartesian grid coordinates for a 3-D unstructured zone where VertexSize is 15.
GridCoordinates_t<1, 15> GridCoordinates =
{{
! DataType = real
! IndexDimension = 1
! DataSize = VertexSize = 15
DataArray_t<real, 1, 15> CoordinateX =
{{
Data(real, 1, 15) = (x(i), i=1,15) ;
}} ;
DataArray_t<real, 1, 15> CoordinateY =
{{
Data(real, 1, 15) = (y(i), i=1,15) ;
}} ;
DataArray_t<real, 1, 15> CoordinateZ =
{{
Data(real, 1, 15) = (z(i), i=1,15) ;
}} ;
}} ;
The Elements_t data structure is required for unstructured zones, and contains the element connectivity data, the element type, the element range, the parent elements data, and the number of boundary elements.
Elements_t :=
{
List( Descriptor_t Descriptor1 ... DescriptorN ) ; (o)
Rind_t<IndexDimension> Rind ; (o/d)
IndexRange_t ElementRange ; (r)
int ElementSizeBoundary ; (o/d)
ElementType_t ElementType ; (r)
DataArray_t<int, 1, ElementDataSize> ElementConnectivity ; (r)
DataArray_t<int, 1, ElementSize + 1> ElementStartOffset ; (r)
DataArray_t<int, 2, [ElementSize, 2]> ParentElements; (o)
DataArray_t<int, 2, [ElementSize, 2]> ParentElementsPosition; (o)
List( UserDefinedData_t UserDefinedData1 ... UserDefinedDataN ) ; (o)
} ;
Notes
Rind is an optional field that indicates the number of rind elements included in the elements data. If Rind is absent, then the DataArray_t structure entities contain only core elements of a zone. If Rind is present, it will provide information on the number of rind elements, in addition to the core elements, that are contained in the DataArray_t structures.
Note that the usage of rind data with respect to the size of the DataArray_t structures is different under Elements_t than elsewhere. For example, when rind coordinate data is stored under GridCoordinates_t, the parameter VertexSize accounts for the core data only. The size of the DataArray_t structures containing the grid coordinates is determined by the DataSize function, which adds the number of rind planes or points to VertexSize. But for the element connectivity, the size of the DataArray_t structures containing the connectivity data is just ElementDataSize, which depends on ElementSize, and includes both the core and rind elements.
ElementRange contains the index of the first and last elements defined in ElementConnectivity. The elements are indexed with a global numbering system, starting at 1, for all element sections under a given Zone_t data structure. The global numbering insures that each element, whether it's a cell, a face, or an edge, is uniquely identified by its number. They are also listed as a continuous list of element numbers within any single element section. Therefore the number of elements in a section is:
ElementSize = ElementRange.end - ElementRange.start + 1
The element indices are used for the boundary condition and zone connectivity definition.
ElementSizeBoundary indicates if the elements are sorted, and how many boundary elements are recorded. By default, ElementSizeBoundary is set to zero, indicating that the elements are not sorted. If the elements are sorted, ElementSizeBoundary is set to the number of elements at the boundary. Consequently:
ElementSizeInterior = ElementSize - ElementSizeBoundary
ElementType_t is an enumeration of the supported element types:
ElementType_t := Enumeration(
ElementTypeNull, ElementTypeUserDefined, NODE, BAR_2, BAR_3,
TRI_3, TRI_6, QUAD_4, QUAD_8, QUAD_9,
TETRA_4, TETRA_10, PYRA_5, PYRA_14,
PENTA_6, PENTA_15, PENTA_18, HEXA_8, HEXA_20, HEXA_27,
MIXED, PYRA_13, NGON_n, NFACE_n,
BAR_4, TRI_9, TRI_10, QUAD_12, QUAD_16,
TETRA_16, TETRA_20, PYRA_21, PYRA_29, PYRA_30,
PENTA_24, PENTA_38, PENTA_40, HEXA_32, HEXA_56, HEXA_64 );
The conventions for element numbering for the various supported types
are described in Unstructured Grid
Element Numbering Conventions.
For all element types except MIXED, ElementConnectivity contains the list of nodes for each element. If the elements are sorted, then it must first list the connectivity of the boundary elements, then that of the interior elements.
ElementConnectivity = Node11, Node21, ... NodeN1,
Node12, Node22, ... NodeN2,
...
Node1M, Node2M, ... NodeNM
where M is the total number of elements (i.e.,
ElementSize), and N is the number of nodes per element.
ElementDataSize indicates the total size (number of integers) of the array ElementConnectivity. For all element types except MIXED, NGON_n, and NFACE_n, ElementDataSize is given by:
ElementDataSize = ElementSize * NPE[ElementType]where NPE[ElementType] is a function returning the number of nodes for the given ElementType. For example, NPE[HEXA_8]=8.
When the section ElementType is MIXED, the data array ElementConnectivity contains one extra integer per element, to hold each individual element type:
ElementConnectivity = Etype1, Node11, Node21, ... NodeN1,
Etype2, Node12, Node22, ... NodeN2,
...
EtypeM, Node1M, Node2M, ... NodeNM
where again M is the total number of elements, and
Ni is the number of nodes in element i.
The data array ElementStartOffset contains the starting positions of each element in the ElementConnectivity data array
and its last value corresponds to the ElementConnectivity total size:
ElementStartOffset = 0, NPE[Etype1] + 1, ... ElementStartOffset[n-1] + NPE[Etypen] + 1,
..., ElementStartOffset[M-1] + NPE[EtypeM] + 1 = ElementDataSize
In the case of MIXED element section, ElementDataSize is
given by:
ElementDataSize = ∑(NPE[ElementTypen] + 1)where the summation is over n, and n represents a specific element type.
Arbitrary polyhedral elements may be defined using the NGON_n and NFACE_n element types. The NGON_n element type is used to specify all the faces in the grid, and the NFACE_n element type is then used to define the polyhedral elements as a collection of these faces. Except for boundary faces, each face of a polyhedral element must be shared by another polyhedral element.
For example, for NGON_n, the data array ElementConnectivity contains a list of nodes making up each face in the grid while ElementStartOffset provides the starting position of each face in the ElementConnectivity array:
ElementConnectivity = Node11, Node21, ... NodeN1,
Node12, Node22, ... NodeN2,
...
Node1M, Node2M, ... NodeNM
ElementStartOffset = 0, Nnodes1, Nnodes1 + Nnodes2, ...
..., ElementStartOffset[i-1] + Nnodesi,
..., ElementStartOffset[M-1] + NnodesM = ElementDataSize
where here M is the total number of faces, and
Nnodesi is the number of nodes in face i.
The ElementDataSize is the total number of nodes defining all
the faces.
Note that the number of nodes in face i is given by:
Nnodesi = ElementStartOffset[i+1] - ElementStartOffset[i]
Then for NFACE_n, ElementConnectivity contains the list of face elements making up each polyhedral element, while ElementStartOffset provides the starting position of each polyhedral element in the ElementConnectivity array:
ElementConnectivity = Face11, Face21, ... FaceN1,
Face12, Face22, ... FaceN2,
...
Face1M, Face2M, ... FaceNM
ElementStartOffset = 0, Nfaces1, Nfaces1 + Nfaces2, ...
..., ElementStartOffset[i-1] + Nfacesi,
..., ElementStartOffset[M-1] + NfacesM = ElementDataSize
where now M is the total number of polyhedral elements, and
Nfacesi is the number of faces in element i.
The sign of the face number determines its orientation (i.e., the
direction of the face normal, constructed as defined by the
convention for 2-D elements).
If the face number is positive, the face normal is directed outward; if
it's negative, the face normal is directed inward.
The ElementDataSize is the sum of the number of faces defining
each polyhedral element.
Note that the number of faces in element i is given by:
Nfacesi = ElementStartOffset[i+1] - ElementStartOffset[i]
For face elements in 3-D, or bar element in 2-D, additonal data may be provided for each element in ParentElements and ParentElementsPosition. The element numbers of the two adjacent cells for each face are given in ParentElements. The corresponding canonical positions of the face in the two parent cells is given in ParentElementsPosition; these canonical face positions are defined in the section Unstructured Grid Element Numbering Conventions. For faces on the boundary of the domain, the second parent is set to zero.
The UserDefinedData_t data structure allows arbitrary user-defined data to be stored in Descriptor_t and DataArray_t children without the restrictions or implicit meanings imposed on these node types at other node locations.
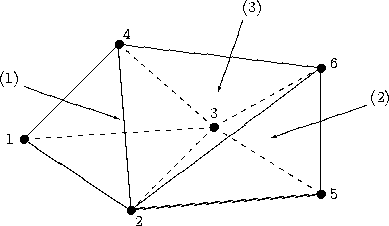
This section contains four examples of elements definition in CGNS. The first example is for a simple three-element tetrahedral grid, using the TETRA_4 element type. The second example is for the same grid as the first example, but the elements are treated as general polyhedra to illustrate the use of the NGON_n and NFACE_n element types. The third and fourth examples are for an unstructured zone with 15 tetrahedral and 10 hexahedral elements, with the third example defining the elements in separate sections for the TETRA_4 and HEXA_8 element types, and the fourth example combining them using the MIXED element type.

The element type is TETRA_4, and the connectivity is defined in ElementConnectivity by specifying the four nodes comprising each element, with the order consistent with the numbering conventions for tetrahedral elements. The data in ElementConnectivity is grouped by element; note that the parentheses are added here for presentation purposes only.
Zone_t UnstructuredZone =
{{
Elements_t TetraElements =
{{
IndexRange_t ElementRange = [1,3] ;
ElementType_t ElementType = TETRA_4 ;
DataArray_t<int, 1, NPE[TETRA_4] × 3> ElementConnectivity =
{{
Data(int, 1, NPE[TETRA_4] × 3) =
(1, 2, 3, 4), (2, 5, 3, 6), (2, 6, 3, 4) ;
}} ;
}} ;
}} ;
This example uses the same grid as in the previous example, but treats the elements as general polyhedra to illustrate the use of the NGON_n and NFACE_n element types. The grid consists of three volume elements, each made up of four face elements, with each face defined by three nodes.
For each face, the nodes comprising that face are listed in ElementConnectivity for the NGON_n element type. The ElementRange is [1,10], corresponding to the 10 total faces in the grid. The ElementDataSize is 30, corresponding to the total of 30 nodes defining the 10 faces.
The faces making up the three volume elements are then listed in ElementConnectivity for the NFACE_n element type. The ElementRange is [11,13], corresponding to the three volume elements. The ElementDataSize is 12, corresponding to three volume elements with four faces per element. Note that the face numbers for faces 3 and 8 are negative in the definition of volume element 3, since their normals point inward for that element. Again, the parentheses in ElementConnectivity are for presentation purposes only.
Zone_t UnstructuredZone =
{{
Elements_t NgonElements =
{{
IndexRange_t ElementRange = [1,10] ;
ElementType_t ElementType = NGON_n ;
DataArray_t<int, 1, 30> ElementConnectivity =
{{
Data(int, 1, 30) =
(1, 3, 2), (1, 2, 4), (2, 3, 4), (3, 1, 4),
(2, 3, 5), (2, 5, 6), (5, 3, 6), (3, 2, 6),
(2, 6, 4), (6, 3, 4) ;
}} ;
DataArray_t<int, 1, 11> ElementStartOffset =
{{
Data(int, 1, 11) =
0, 3, 6, 9,
12, 15, 18, 21,
24, 27, 30 ;
}} ;
}} ;
Elements_t NfaceElements =
{{
IndexRange_t ElementRange = [11,13] ;
ElementType_t ElementType = NFACE_n ;
DataArray_t<int, 1, 12> ElementConnectivity =
{{
Data(int, 1, 12) =
( 1, 2, 3, 4),
( 5, 6, 7, 8),
(-8, 9, 10, -3) ;
}} ;
DataArray_t<int, 1, 4> ElementStartOffset =
{{
Data(int, 1, 4) =
0, 4, 8, 12 ;
}} ;
}} ;
}} ;
In this example, elements are defined for an unstructured zone with 15 tetrahedral and 10 hexahedral elements. The elements are written in two separate sections, one for the tetrahedral elements and one for the hexahedral elements.
Zone_t UnstructuredZone =
{{
Elements_t TetraElements =
{{
IndexRange_t ElementRange = [1,15] ;
int ElementSizeBoundary = 10 ;
ElementType_t ElementType = TETRA_4 ;
DataArray_t<int, 1, NPE[TETRA_4] × 15> ElementConnectivity =
{{
Data(int, 1, NPE[TETRA_4] × 15) = (node(i,j), i=1,NPE[TETRA_4], j=1,15) ;
}} ;
}} ;
Elements_t HexaElements =
{{
IndexRange_t ElementRange = [16,25] ;
int ElementSizeBoundary = 0 ;
ElementType_t ElementType = HEXA_8 ;
DataArray_t<int, 1, NPE[HEXA_8] × 10> ElementConnectivity =
{{
Data(int, 1, NPE[HEXA_8] × 10) = (node(i,j), i=1,NPE[HEXA_8], j=1,10) ;
}} ;
}} ;
}} ;
In this example, the same unstructured zone described in the previous example is written in a single element section of type MIXED (i.e., an unstructured grid composed of mixed elements).
Zone_t UnstructuredZone =
{{
Elements_t MixedElementsSection =
{{
IndexRange_t ElementRange = [1,25] ;
ElementType_t ElementType = MIXED ;
DataArray_t<int, 1, ElementDataSize> ElementConnectivity =
{{
Data(int, 1, ElementDataSize) = (etype(j),(node(i,j),
i=1,NPE[etype(j)]), j=1,25) ;
}} ;
}} ;
DataArray_t<int, 1, 26> ElementStartOffset =
{{
Data(int, 1, 26) =
0, (NPE[etype(j)]+ElementStartOffset[j], j=1,25) ;
}} ;
}} ;
The Axisymmetry_t data structure allows recording the axis of rotation and the angle of rotation around this axis for a two-dimensional dataset that represents an axisymmetric database.
Axisymmetry_t :=
{
List( Descriptor_t Descriptor1 ... DescriptorN ) ; (o)
DataArray_t<real,1,2> AxisymmetryReferencePoint ; (r)
DataArray_t<real,1,2> AxisymmetryAxisVector ; (r)
DataArray_t<real,1,1> AxisymmetryAngle ; (o)
DataArray_t<char,2,[32,2]> CoordinateNames ; (o)
DataClass_t DataClass ; (o)
DimensionalUnits_t DimensionalUnits ; (o)
List( UserDefinedData_t UserDefinedData1 ... UserDefinedDataN ) ; (o)
} ;
Notes
AxisymmetryReferencePoint specifies the origin used for defining the axis of rotation.
AxisymmetryAxisVector contains the direction cosines of the axis of rotation, through the AxisymmetryReferencePoint. For example, for a 2-D dataset defined in the (x,y) plane, if AxisymmetryReferencePoint contains (0,0) and AxisymmetryAxisVector contains (1,0), the x-axis is the axis of rotation.
AxisymmetryAngle allows specification of the circumferential extent about the axis of rotation. If this angle is undefined, it is assumed to be 360°.
CoordinateNames may be used to specify the first and second coordinates used in the definition of AxisymmetryReferencePoint and AxisymmetryAxisVector. If not found, it is assumed that the first coordinate is CoordinateX and the second is CoordinateY. The coordinates given under CoordinateNames, or implied by using the default, must correspond to those found under GridCoordinates_t.
DataClass defines the default class for numerical data contained in the DataArray_t entities. For dimensional data, DimensionalUnits may be used to describe the system of units employed. If present, these two entities take precedence over the corresponding entities at higher levels of the CGNS hierarchy, following the standard precedence rules.
The UserDefinedData_t data structure allows arbitrary user-defined data to be stored in Descriptor_t and DataArray_t children without the restrictions or implicit meanings imposed on these node types at other node locations.
The RotatingCoordinates_t data structure is used to record the rotation center and rotation rate vector of a rotating coordinate system.
RotatingCoordinates_t :=
{
List( Descriptor_t Descriptor1 ... DescriptorN ) ; (o)
DataArray_t<real,1,PhysicalDimension> RotationCenter ; (r)
DataArray_t<real,1,PhysicalDimension> RotationRateVector ; (r)
DataClass_t DataClass ; (o)
DimensionalUnits_t DimensionalUnits ; (o)
List( UserDefinedData_t UserDefinedData1 ... UserDefinedDataN ) ; (o)
} ;
Notes
RotationCenter specifies the coordinates of the center of rotation, and RotationRateVector specifies the components of the angular velocity of the grid about the center of rotation. Together, they define the angular velocity vector. The direction of the angular velocity vector specifies the axis of rotation, and its magnitude specifies the rate of rotation.
For example, for the common situation of rotation about the x-axis, RotationCenter would be specified as any point on the x-axis, like (0,0,0). RotationRateVector would then be specified as (ω,0,0), where ω is the rotation rate. Using the right-hand rule, ω would be positive for clockwise rotation (looking in the +x direction), and negative for counter-clockwise rotation.
Note that for a rotating coordinate system, the axis of rotation is defined in the inertial frame of reference, while the grid coordinates stored using the GridCoordinates_t data structure are relative to the rotating frame of reference.
DataClass defines the default class for data contained in the DataArray_t entities. For dimensional data, DimensionalUnits may be used to describe the system of units employed. If present, these two entities take precedence over the corresponding entities at higher levels of the CGNS hierarchy, following the standard precedence rules.
The UserDefinedData_t data structure allows arbitrary user-defined data to be stored in Descriptor_t and DataArray_t children without the restrictions or implicit meanings imposed on these node types at other node locations.
If rotating coordinates are used, it is useful to store variables relative to the rotating frame. Standardized data-name identifiers should be used for these variables, as defined for flow-solution quantities in the section Conventions for Data-Name Identifiers.
The flow solution within a given zone is described by the FlowSolution_t structure. This structure contains a list for the data arrays of the individual flow-solution variables, as well as identifying the grid location of the solution. It also provides a mechanism for identifying rind-point data included within the data arrays.
FlowSolution_t< int CellDimension, int IndexDimension,
int VertexSize[IndexDimension],
int CellSize[IndexDimension] > :=
{
List( Descriptor_t Descriptor1 ... DescriptorN ) ; (o)
GridLocation_t GridLocation ; (o/d)
Rind_t<IndexDimension> Rind ; (o/d)
IndexRange<IndexDimension> PointRange ; (o)
IndexArray<IndexDimension, ListLength[], int> PointList ; (o)
List( DataArray_t<DataType, IndexDimension, DataSize[]>
DataArray1 ... DataArrayN ) ; (o)
DataClass_t DataClass ; (o)
DimensionalUnits_t DimensionalUnits ; (o)
List( UserDefinedData_t UserDefinedData1 ... UserDefinedDataN ) ; (o)
} ;
Notes
FlowSolution_t requires four structure parameters; CellDimension identifies the dimensionality of cells or elements, IndexDimension identifies the dimensionality of the grid-size arrays, and VertexSize and CellSize are the number of core vertices and cells, respectively, in each index direction, excluding rind points. For structured zones, core vertices and cells begin at [1,1,1] (in 3-D) and end at VertexSize and CellSize, respectively. For unstructured zones, IndexDimension is always 1.
The flow solution data is stored in the list of DataArray_t entities; each DataArray_t structure entity may contain a single component of the solution vector. Standardized data-name identifiers for the flow-solution quantities are described in the section Conventions for Data-Name Identifiers. The field GridLocation specifies the location of the solution data with respect to the grid; if absent, the data is assumed to coincide with grid vertices (i.e., GridLocation = Vertex). All data within a given instance of FlowSolution_t must reside at the same grid location.
For structured grids, the value of GridLocation alone specifies the location and indexing of the flow solution data. Vertices are explicity indexed. Cell centers and face centers are indexed using the minimum of the connecting vertex indices, as described in the section Structured Grid Notation and Indexing Conventions.
For unstructured grids, the value of GridLocation alone specifies location and indexing of flow solution data only for vertex and cell-centered data. The reason for this is that element-based grid connectivity provided in the Elements_t data structures explicitly indexes only vertices and cells. For data stored at alternate grid locations (e.g., edges), additional connectivity information is needed. This is provided by the optional fields PointRange and PointList; these refer to vertices, edges, faces or cell centers, depending on the values of CellDimension and GridLocation. The following table shows these relations. The NODE element type should not be used in place of the vertex. A vertex GridLocation should use the GridLocation = Vertex pattern, which implies an indexing on the grid coordinates arrays and not a NODE Elements_t array.
| CellDimension | GridLocation | |||
|---|---|---|---|---|
| Vertex | EdgeCenter | *FaceCenter | CellCenter | |
| 1 | vertices | - | - | cells (line elements) |
| 2 | vertices | edges | - | cells (area elements) |
| 3 | vertices | edges | faces | cells (volume elements) |
Note: In the table, *FaceCenter stands for the possible types: IFaceCenter, JFaceCenter, KFaceCenter, or FaceCenter.
Although intended for edge or face-based solution data for unstructured grids, the fields PointRange/List may also be used to (redundantly) index vertex and cell-centered data. In all cases, indexing of flow solution data corresponds to the element numbering as defined in the Elements_t data structures.
Rind is an optional field that indicates the number of rind planes (for structured grids) or rind points or elements (for unstructured grids) included in the data. Its purpose and function are identical to those described for the GridCoordinates_t structure. Note, however, that the Rind in this structure is independent of the Rind contained in GridCoordinates_t. They are not required to contain the same number of rind planes or elements. Also, the location of any flow-solution rind points is assumed to be consistent with the location of the core flow solution points (e.g., if GridLocation = CellCenter, rind points are assumed to be located at fictitious cell centers).
DataClass defines the default class for data contained in the DataArray_t entities. For dimensional flow solution data, DimensionalUnits may be used to describe the system of units employed. If present, these two entities take precedence over the corresponding entities at higher levels of the CGNS hierarchy, following the standard precedence rules.
The UserDefinedData_t data structure allows arbitrary user-defined data to be stored in Descriptor_t and DataArray_t children without the restrictions or implicit meanings imposed on these node types at other node locations.
FlowSolution_t requires the structure function ListLength, which is used to specify the number of entities (e.g. vertices) corresponding to a given PointRange or PointList. If PointRange is specified, then ListLength is obtained from the number of points (inclusive) between the beginning and ending indices of PointRange. If PointList is specified, then ListLength is the number of indices in the list of points. In this situation, ListLength becomes a user input along with the indices of the list PointList. By user we mean the application code that is generating the CGNS database.
The function DataSize[] is the size of flow solution data arrays. If Rind is absent then DataSize represents only the core points; it will be the same as VertexSize or CellSize depending on GridLocation. The definition of the function DataSize[] is as follows:
if (PointRange/PointList is present) then
{
DataSize[] = ListLength[] ;
}
else if (Rind is absent) then
{
if (GridLocation = Vertex) or (GridLocation is absent)
{
DataSize[] = VertexSize[] ;
}
else if (GridLocation = CellCenter) then
{
DataSize[] = CellSize[] ;
}
}
else if (Rind is present) then
{
if (GridLocation = Vertex) or (GridLocation is absent) then
{
DataSize[] = VertexSize[] + [a + b,...] ;
}
else if (GridLocation = CellCenter)
{
DataSize[] = CellSize[] + [a + b,...] ;
}
}
where RindPlanes = [a,b,...] (see the
Rind_t structure for the
definition of RindPlanes).
This section contains an example of the flow solution entity, including the designation of grid location and rind planes and data-normalization mechanisms.
Conservation-equation variables (ρ, ρu, ρv, and ρe0) for a 2-D grid of size 11 × 5. The flowfield is cell-centered with two planes of rind data. The density, momentum and stagnation energy (ρe0) data is nondimensionalized with respect to a freestream reference state whose quantities are dimensional. The freestream density and pressure are used for normalization; these values are 1.226 kg/m3 and 1.0132×105 N/m2 (standard atmosphere conditions). The data-name identifier conventions for the conservation-equation variables are Density, MomentumX, MomentumY and EnergyStagnationDensity.
! CellDimension = 2
! IndexDimension = 2
! VertexSize = [11,5]
! CellSize = [10,4]
FlowSolution_t<2, [11,5], [10,4]> FlowExample =
{{
GridLocation_t GridLocation = CellCenter ;
Rind_t<2> Rind =
{{
int[4] RindPlanes = [2,2,2,2] ;
}} ;
DataClass_t DataClass = NormalizedByDimensional ;
DimensionalUnits_t DimensionalUnits =
{{
MassUnits = Kilogram ;
LengthUnits = Meter ;
TimeUnits = Second ;
TemperatureUnits = TemperatureUnitsNull ;
AngleUnits = AngleUnitsNull ;
}} ;
! DataType = real
! Dimension = 2
! DataSize = CellSize + [4,4] = [14,8]
DataArray_t<real, 2, [14,8]> Density =
{{
Data(real, 2, [14,8]) = ((rho(i,j), i=-1,12), j=-1,6) ;
DataConversion_t DataConversion =
{{
ConversionScale = 1.226 ;
ConversionOffset = 0 ;
}} ;
DimensionalExponents_t DimensionalExponents =
{{
MassExponent = +1 ;
LengthExponent = -3 ;
TimeExponent = 0 ;
TemperatureExponent = 0 ;
AngleExponent = 0 ;
}} ;
}} ;
DataArray_t<real, 2, [14,8]> MomentumX =
{{
Data(real, 2, [14,8]) = ((rho_u(i,j), i=-1,12), j=-1,6) ;
DataConversion_t DataConversion =
{{
ConversionScale = 352.446 ;
ConversionOffset = 0 ;
}} ;
}} ;
DataArray_t<real, 2, [14,8]> MomentumY =
{{
Data(real, 2, [14,8]) = ((rho_v(i,j), i=-1,12), j=-1,6) ;
DataConversion_t DataConversion =
{{
ConversionScale = 352.446 ;
ConversionOffset = 0 ;
}} ;
}} ;
DataArray_t<real, 2, [14,8]> EnergyStagnationDensity =
{{
Data(real, 2, [14,8]) = ((rho_e0(i,j), i=-1,12), j=-1,6) ;
DataConversion_t DataConversion =
{{
ConversionScale = 1.0132e+05 ;
ConversionOffset = 0 ;
}} ;
}} ;
}} ;
The value of GridLocation
indicates the data is at cell centers, and the value of
RindPlanes specifies two rind
planes on each face of the zone.
The resulting value of the structure function
DataSize is the number of cells
plus four in each coordinate direction; this value is passed to each of
the DataArray_t entities.
Since the data are all nondimensional and normalized by dimensional reference quantities, this information is stated in DataClass and DimensionalUnits at the FlowSolution_t level rather than attaching the appropriate DataClass and DimensionalUnits to each DataArray_t entity. It could possibly be at even higher levels in the heirarchy. The contents of DataConversion are in each case the denominator of the normalization; this is ρ∞ for density, (p∞ ρ∞)1/2 for momentum, and p∞ for stagnation energy. The dimensional exponents are specified for density. For all the other data, the dimensional exponents are to be inferred from the data-name identifiers.
Note that no information is provided to identify the actual reference state or indicate that it is freestream. This information is not needed for data manipulations involving renormalization or changing the units of the converted raw data.
ZoneSubRegion_t< int IndexDimension, int CellDimension > :=
{
List( Descriptor_t Descriptor1 ... DescriptorN ) ; (o)
int RegionCellDimension ; (o/d)
GridLocation_t GridLocation ; (o/d)
IndexRange_t<IndexDimension> PointRange ; (r:o:o:o)
IndexArray_t<IndexDimension, ListLength, int> PointList ; (o:r:o:o)
Descriptor_t BCRegionName ; (o:o:r:o)
Descriptor_t GridConnectivityRegionName ; (o:o:o:r)
Rind_t<IndexDimension> Rind; (o/d)
List( DataArray_t<DataType, 1, ListLength[]> DataArray1 ... DataArrayN ) ; (o)
FamilyName_t FamilyName ; (o)
List( AdditionalFamilyName_t AddFamilyName1 ... AddFamilyNameN ) ; (o)
DataClass_t DataClass ; (o)
DimensionalUnits_t DimensionalUnits ; (o)
List( UserDefinedData_t UserDefinedData1 ... UserDefinedDataN ) ; (o)
} ;
Notes
The extent of the subregion and the distribution of data within that subregion is determined by RegionCellDimension, GridLocation, and one of PointRange/List, BCRegionName, or GridConnectivityRegionName. For a 3-D subregion (RegionCellDimension = 3), data can be located at vertices, edges, face centers or cell centers. For a 2-D subregion (RegionCellDimension = 2), data can be located at vertices, edges or cell centers (i.e. area elements). It is anticipated that one of the widest uses for ZoneSubRegion_t will be to store specific boundary-only information. For example, in a 3-D simulation, one may wish to store additional data on surfaces. In this case, the RegionCellDimension would be set to 2.
PointRange/List refer to vertices, edges, faces or cell centers, depending on the values of RegionCellDimension and GridLocation. Note that it is both the dimensionality of the zone (CellDimension) as well as the dimensionality of the subregion (RegionCellDimension), that determines the types of elements permissible in PointRange/List. The following table shows these relations.
| CellDimension | RegionCellDimension | GridLocation | |||
|---|---|---|---|---|---|
| Vertex | EdgeCenter | *FaceCenter | CellCenter | ||
| 1 | 1 | vertices | - | - | cells (line elements) |
| 2 | 1 | vertices | edges | - | - |
| 2 | 2 | vertices | edges | - | cells (area elements) |
| 3 | 1 | vertices | edges | - | - |
| 3 | 2 | vertices | edges | faces | - |
| 3 | 3 | vertices | edges | faces | cells (volume elements) |
Note: In the table, *FaceCenter stands for the possible types: IFaceCenter, JFaceCenter, KFaceCenter, or FaceCenter.
For both structured and unstructured grids, GridLocation = Vertex means that PointRange/List refers to vertex indices. For structured grids, edges, faces and cell centers are indexed using the minimum of the connecting vertex indices, as described in the section Structured Grid Notation and Indexing Conventions. For unstructured grids, edges, faces and cell centers are indexed using their element numbering, as defined in the Elements_t data structures.
If the vertices or elements of the subregion are continuously numbered, then PointRange may be used. Otherwise, PointList should be used to list the vertices/elements. Alternatively, if the data locations and range of the subregion coincide with an existing BC region or zone-to-zone GridConnectivity region, then BCRegionName or GridConnectivityRegionName may be used. BCRegionName is a string giving the name of an existing BC_t node of the current zone. GridConnectivityRegionName is a string giving the name of an existing GridConnectivity1to1_t or GridConnectivity_t node of the current zone. The name referred to should be unambiguous.
Consistent with FlowSolution_t, the subregionís solution data is stored in the list of DataArray_t entities; each DataArray_t structure entity contains a single quantity. Standardized data-name identifiers for solution quantities are described in the section Conventions for Data-Name Identifiers. As noted above, all solution data within a given subregion must reside at the same grid location.
DataClass defines the default class for data contained in the DataArray_t entities. For dimensional flow solution data, DimensionalUnits may be used to describe the system of units employed. If present, these two entities take precedence over the corresponding entities at higher levels of the CGNS hierarchy, following the standard precedence rules.
ZoneSubRegion_t requires the structure function ListLength[], which is used to specify the number of data points (e.g. vertices, cell centers, face centers, edge centers) corresponding to the given PointRange/List. If PointRange is specified, then ListLength is obtained from the number of points (inclusive) between the beginning and ending indices of PointRange. If PointList is specified, then ListLength is the number of indices in the list of points. In this situation, ListLength becomes a user input along with the indices of the list PointList. By user we mean the application code that is generating the CGNS database.
Rind is an optional field that indicates the number of rind planes (for structured grids) or rind points (for unstructured grids). If Rind is absent, then the DataArray_t structure entities contain only core data of length ListLength, as defined for this region. If Rind is present, it will provide information on the number of rind elements, in addition to the ListLength, that are contained in the DataArray_t structures. The bottom line is that Rind simply adds a specified number to ListLength, as used by the DataArray_t structures.
The UserDefinedData_t data structure allows arbitrary user-defined data to be stored.
There may be multiple instances of ZoneSubRegion_t in a given zone. These may simply be multiple regions defined for a single solution, or they may be associated with different times / different solutions in a time-dependent simulation (in which case ZoneIterativeData should be used to associate them).
All FamilyName and AdditionalFamilyName entries should respect the rules defined in Base Level Families and Zone_t.
This section contains four examples of Zone Subregions, including the use of PointList, PointRange and BCRegionName.
Under Zone_t:
ZoneSubRegion_t<3,3> Region1 =
{{
GridLocation_t GridLocation = CellCenter ;
int RegionCellDimension = 3;
IndexRange_t<3> PointRange =
{{
int[3] Begin = [121,17,21];
int[3] End = [149,45,21];
}};
! ListLength = (149-121+1)*(45-17+1)*(23-21+1) = 29*29*3 = 2523
DataArray_t<real,1,2523> Temperature =
{{
Data(real,1,2523) = temperature at the cell centers specified
}} ;
DataArray_t<real,1,2523> ViscosityKinematic =
{{
Data(real,1,2523) = kinematic viscosity at the cell centers specified
}} ;
}} ; ! end Region1
Under Zone_t:
ZoneSubRegion_t<1,3> Region1 =
{{
GridLocation_t GridLocation = CellCenter ;
int RegionCellDimension = 3;
IndexArray_t<1,2523,int> PointList =
{{
int[1] ElementList = list of 3-D element numbers where region data given
}} ;
! ListLength = length of the element list = 2523
DataArray_t<real,1,2523> Temperature =
{{
Data(real,1,2523) = temperature at the element cell centers specified
}} ;
DataArray_t<real,1,2523> ViscosityKinematic =
{{
Data(real,1,2523) = kinematic viscosity at the element cell centers specified
}} ;
}} ; ! end Region1
Under Zone_t:
ZoneSubRegion_t<1,3> Region1 =
{{
GridLocation_t GridLocation = FaceCenter ;
int RegionCellDimension = 2;
IndexArray_t<1,25,int> PointRange =
{{
int[1] Begin = [5568];
int[1] End = [5592];
}} ;
! ListLength = length of the element list = 25
DataArray_t<real,1,25> Temperature =
{{
Data(real,1,25) = temperature at the specific face element locations specified
}} ;
DataArray_t<real,1,25> ViscosityKinematic =
{{
Data(real,1,25) = kinematic viscosity at the specific face element locations specified
}} ;
}} ; ! end Region1
Under Zone_t:
ZoneSubRegion_t<1,3> Region1 =
{{
int RegionCellDimension = 2;
Descriptor_t BCRegionName = "name of a ZoneBC/BC_t node" ;
! ListLength = length of the point/element list from BC_t = 25
DataArray_t<real,1,25> Temperature =
{{
Data(real,1,25) = temperature at the specific BC locations specified
}} ;
DataArray_t<real,1,25> ViscosityKinematic =
{{
Data(real,1,25) = kinematic viscosity at the specific BC locations specified
}} ;
}} ; ! end Region1